Does the Altitude of an Equilateral Triangle Bisect the Base

In every other triangle the altitude does not bisect the base. It bisects the base of the triangle and always lies inside the triangle.

Geometry Is It Safe To Assume That The Altitude Of A Triangle Always Cuts The Base In Half Mathematics Stack Exchange

ADC and CDB are equal because the have two sides equal and one angle equal SAS then ADDB hence the altitude bisects the base.

. Does the Altitude of a Triangle Always Make 90 With the Base of the Triangle. An altitude from a vertex bisects the opposite base if and only if the two sides emerging from that particular vertex are equalnot necessary in a right angle triangleTherefore you need to specify this condition before assuming that the altitude cuts. The area it will be defined by the following formula.

Try to prove all these properties on your own. The intersection of the extended base and the altitude is called the foot of the altitude. When the altitude to the base of an isosceles triangle is drawn two congruent triangles are formed proven by Hypotenuse - Leg.

That the angle bisector is perpendicular to the base in an isosceles triangle. It is interesting to note that the altitude of an equilateral triangle bisects its base and the opposite angle. The measure of the side length2 - The measure of the one half of the base length 2 The measure of the altitude2.

Thus from the above figure we can find the height h of the equilateral triangle as. _____ 51 Isosceles Equilateral Triangles An altitude is a perpendicular segment from a vertex to the line containing the opposite side. Altitudes can sometimes coincide with a side of the triangle or can sometimes meet an extended base outside the triangle.

In geometry an altitude of a triangle is a line segment through a vertex and perpendicular to a line containing the base. In the diagram ABC is an isoscels triangle with the congruent sides and and is the median drawn to the base Since corresponding parts of congruent triangles are congruent that means ABD CBDSince the median is the common side of these adjacent angles in fact bisects the vertex angle of the isosceles triangle. In an isosceles triangle the median is also the altitude.

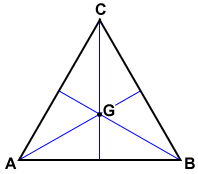
The three altitudes extending from the vertices A B and C of ABC above intersect at point G. Here we will show the opposite. A few things this.

Label 442 An alternative straight path splits the triangle into a trapezoid and a small. If median drawn from vertex A is also the angle bisector the triangle is isosceles such that AB AC and BC is the base. As we know an equilateral triangle has all equal sides.

The image below shows an equilateral triangle ABC where BD is the height h AB BC AC ABD CBD and AD CD. So if the altitude of an equilateral triangle is. In this proof and in all similar problems related to the properties of an isosceles triangle we employ the same basic strategy.

Now if we drop an altitude from the apex of the triangle to the base it divides the triangle into two equal right triangles. As in any type of triangle its area is equal to half of the product of its base and height. Hence this median is also the altitude.

With these two facts in hand it will be easy to show several other properties of isosceles triangles using the same method triangle congruency. The simplest bisecting path is a vertical segment that splits the triangle into two right triangles each with base 12. That way you will not forget them.

This path is the triangles altitude and it has length. An equilateral triangle has three equal sides and angles. This line containing the opposite side is called the extended base of the altitude.

Area of an Equilateral Triangle. From what I deduced from Wikipedia is that this is only true if the triangle is either isosceles or a right triangle is not fully correct. The length of the altitude often simply called the altitude is the distance between the.

In Figure 2 AC is an altitude to base BC and BC is an altitude to base AC. Lets start by proving that in. Altitudes of equilateral triangles.

L sqrt 1 2 - 12 2 frac sqrt 3 2 0866. Only in an equilateral ET and isosceles triangle IT would that be true and in the isosceles the non-equal side would have to be the base. We use congruent triangles to show.

It is also called altitude of an equilateral triangle. Answer 1 of 2. That depends how perpendicular is drawn if perpendicular is drawn from opposite vertex it will be an Altitude and if it bisects the base of a.

The altitude to the base of an isosceles triangle bisects the vertex angle. The altitude to the base of an isosceles triangle bisects the base. In an equilateral triangle a triangle with three equal sides an altitude cuts any side perfectly in half meaning this is now called the altitude bisector.

An altitude of an equilateral triangle is also an angle bisector median and perpendicular bisector. Figure 2 In a right triangle each leg can serve as an altitude. Figure 3 An altitude for an obtuse.

And so on III. In Figure 3 AM is the altitude to base BC. You can find it by using the Pythagorean theorem if you know the side and the base of triangle.

In an equilateral triangle each altitude median and angle bisector drawn from the same vertex overlap. Yes the altitude of a triangle is a perpendicular line segment drawn from a vertex of a triangle. This means the angle bisector is also the height to the base.

CD is the altitude from vertex C to base AB. The three altitudes of an equilateral triangle intersect at a single point. In general altitudes medians and angle bisectors are different segmentsIn certain triangles though they can be the same segmentsIn Figure the altitude drawn from the vertex angle of an isosceles triangle can be proven to be a median as well as an angle bisector.

The altitude to the base of an isosceles triangle bisects the base. Also in the ET and IT where the. The altitude or height of an equilateral triangle is the line segment from a vertex that is perpendicular to the opposite side.

Having proven the Base Angles Theorem for isosceles triangles using triangle congruency we know that in an isosceles triangle the legs are equal and the base angles are congruent. An obelisk is a tall thin four sided monument that tapers to a pyramidal top. Since the altitudes are the angle bisectors medians and perpendicular bisectors point.

Does The Altitude Of A Triangle Always Bisect The Base Of Any Type Of Triangle Or Are There Any Conditions Quora

Equilateral Triangle

Altitude Of A Triangle Definition Formulas Properties Examples